
|
neuroproject.ru
Форум сайта компании НейроПроект
|
| Предыдущая тема :: Следующая тема |
| Автор |
Сообщение |
archic
Новый посетитель

Зарегистрирован: 17 Окт 2006
Сообщения: 2
|
 Добавлено: Вт Окт 17, 2006 3:09 pm Заголовок сообщения: модель Хопфилда и энергия сети Добавлено: Вт Окт 17, 2006 3:09 pm Заголовок сообщения: модель Хопфилда и энергия сети |
 |
|
Прочитав некоторое количество книжек по нейросетеям пришел к выводу, что оптимизацию принято проводить при помощи сетей Хопфилда и восходящих к ним машин Больцмана/Коши. У Терехова, да и в другой литературе описывается, что в ходе работы сеть минимизирует функцию энергии сети E. Часто встречается пример задачи комивояжера, в которой загадочным образом появляется начальная матрица весов, после этого выполняется итеративный процесс в котором минимизируется целевая функция E.
Задача, для которой я хочу приспособить нейронные сети велика, но для начала мне хотелось бы потренироваться и решить небольшую задачу. Например, поиск минимального элемента в массиве, который заполняется случайными числами. Для этого хочется приспособить сеть Хопфилда. Кто-нибудь знает какова возможная схема решения подобной задачи?
Спасибо! |
|
| Вернуться к началу |
|
 |
Victor G. Tsaregorodtsev
Эксперт

Зарегистрирован: 28 Июн 2005
Сообщения: 114
Откуда: Красноярск
|
 Добавлено: Ср Окт 18, 2006 10:28 am Заголовок сообщения: Re: модель Хопфилда и энергия сети Добавлено: Ср Окт 18, 2006 10:28 am Заголовок сообщения: Re: модель Хопфилда и энергия сети |
 |
|
| archic писал(а): | | поиск минимального элемента в массиве, который заполняется случайными числами. Для этого хочется приспособить сеть Хопфилда. |
Да, сэр знает толк в извращениях...
Нейросетевое решение задачи поиска минимума/максимума в массиве было описано кажется в книге Галушкина "Нейроматематика". Реально же там нет ничего нейросетевого (только обзывание нейросетевыми терминами).
Задачу коммивояжера можно решать и при помощи так называемых elastic snake, elastic ring - во многом близкой к сеткам Кохонена нейроархитектуры, минимизирующей длину растягиваемой цепочки ребер циклического графа и сумму расстояний от вершин этого графа до пунктов назначения. Т.е. оптимизация на Хопфилде и Больцмане - это только пара возможных подходов и только для определенного класса задач, а для других задач используются другие варианты сеток и функций энергии.
_________________
www.neuropro.ru - нейросети, анализ данных, прогнозирование |
|
| Вернуться к началу |
|
 |
Oleg Agapkin
Администратор


Зарегистрирован: 10 Июн 2005
Сообщения: 112
Откуда: Москва
|
 Добавлено: Ср Окт 18, 2006 9:57 pm Заголовок сообщения: Добавлено: Ср Окт 18, 2006 9:57 pm Заголовок сообщения: |
 |
|
В той же "Нейроматематике" есть еще и ссылки на статьи, в которых описываются подобные задачи.
В целом же присоединяюсь к словам об "извращениях"
И еще. Мой личный опыт работы с сетями Хопфилда говорит о том, что данный вид сетей хорош в показательных задачах, когда легко можно указать энергетическую функцию. Когда дело доходит до практики, то удается довольно быстро получить первые положительные результаты, но вот дальнейшее улучшение решений упирается в "танцы с бубном" вокруг задания матрицы связей и , зачастую, найти способ задания этой матрицы для устойчивых и качественных решений так и не удается. |
|
| Вернуться к началу |
|
 |
Oleg Agapkin
Администратор


Зарегистрирован: 10 Июн 2005
Сообщения: 112
Откуда: Москва
|
 Добавлено: Чт Окт 19, 2006 6:58 am Заголовок сообщения: Добавлено: Чт Окт 19, 2006 6:58 am Заголовок сообщения: |
 |
|
| Цитата: | | Часто встречается пример задачи комивояжера, в которой загадочным образом появляется начальная матрица весов, после этого выполняется итеративный процесс в котором минимизируется целевая функция E. |
Она появляется не загадочным образом, а вполне осмысленно определяется самим пользователем. Конкретно в самом простом варианте задачи коммивояжера энергия складывается из нескольких слагаемых, часть из которых определяют правильность решения задачи (каждый город обязательно должен быть посещен; каждый город должен быть посещен не более одного раза). Остальные слагаемые определяют зависимость энергии сети от выбранного маршрута.
При каждом слагаемом стоят коэффициенты, которые нужно правильно настроить, чтобы сеть и маршрут оптимальный искала и обошла все города по одному разу. Вот это как раз самое сложное (о чем я упоминал в предыдущем сообщении)
 Вот как в самом простом виде записывается энергия сети Хопфилда для задачи коммивояжера: Вот как в самом простом виде записывается энергия сети Хопфилда для задачи коммивояжера:
Пусть у нас есть N городов, которые необходимо обойти. Зададим матрицу решений N*N, в которой по вертикали будут перечислены города, а по горизонтали - позиции городов в маршруте
При этом
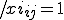 если город если город 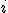 присутствует в маршруте на присутствует в маршруте на 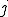 -ой позиции. -ой позиции.
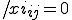 если город если город 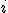 не присутствует в маршруте на не присутствует в маршруте на 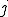 -ой позиции. -ой позиции.
Требования к решению и их матричная интерпретация:
1. Каждый город посещается только один раз. В каждой строке матрицы одна единица, все остальные - нули
2. На каждом месте маршрута не более одного города. В каждом столбце матрицы одна единица, все остальные - нули
3. В маршруте присутствуют N городов. Сумма всех элементов матрицы = N
Тогда энергия сети записывается следующим образом:
Эта формула и есть нейропостановка задачи. Первое слагаемое отвечает первому требования, второе-второму и третье слагаемое отвечает за третье требование.
Эти три первых слагаемых - требование к решению на адекватность. При эволюции сети эти слагаемые не должны дать сети залезть в пространство заведомо неправильных решений (например, выкинуть город из маршрута). Как видно, строгих требований на правильность тут нет. Мы задаем функцию энергии исходя из априорных соображений о том, каким должно быть решение. Мы определяем ее так, чтобы энергия сети при неадекватных решениях была велика.
Последнее слагаемое - это длина маршрута.
Коэффициенты  , , 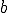 , ,  , , 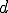 задаются пользователем. Это и есть самое сложное задаются пользователем. Это и есть самое сложное
Аналогичным образом с помощью сетей Хопфилда решается задача n-Ферзей. |
|
| Вернуться к началу |
|
 |
archic
Новый посетитель

Зарегистрирован: 17 Окт 2006
Сообщения: 2
|
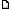 Добавлено: Пн Окт 23, 2006 6:56 pm Заголовок сообщения: Добавлено: Пн Окт 23, 2006 6:56 pm Заголовок сообщения: |
 |
|
| Oleg Agapkin писал(а): | | Когда дело доходит до практики, то удается довольно быстро получить первые положительные результаты, но вот дальнейшее улучшение решений упирается в "танцы с бубном" вокруг задания матрицы связей и , зачастую, найти способ задания этой матрицы для устойчивых и качественных решений так и не удается. |
Уже почувствовал эти трудности при преобразовании целевой функции в функцию энергии и переводе ограничений в множители Лагранжа.. Как же тогда лучше решать сложные оптимизационные задачи нейросетками?
В целом моя задача выглядит так: В трехмерном пространстве есть робот-змея (избыточный манипулятор), которая состоит из звеньев. Каждое звено может поворачиваться на одинаковый телесный угол. Есть цель, начальная позиция робота и множество препятствий. В результате работы начальное звено робот а остается в начальной позиции, а конец последнего звена касается цели.
Решал эту проблему ч/з ГА, там все просто.. Каким образом можно решить ее нейросетью, и можно ли вообще? Какими еще способами можно попытаться решить эту проблему кроме ГА? |
|
| Вернуться к началу |
|
 |
|
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
|
|








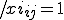 если город
если город 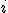 присутствует в маршруте на
присутствует в маршруте на 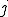 -ой позиции.
-ой позиции.
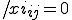 если город
если город  ,
, 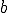 ,
,  ,
, 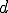 задаются пользователем. Это и есть самое сложное
задаются пользователем. Это и есть самое сложное